Ejemplo 1
El vector es combinación lineal de ya que:
Veamos cómo se puede pensar esto desde la perspectiva geométrica. ¿Qué vectores pueden expresarse como combinación lineal del vector ?
Todos los vectores con . Es decir que todos los vectores sobre el eje , son combinación lineal de .
Ejemplo 2
El vector es combinación lineal de ya que:
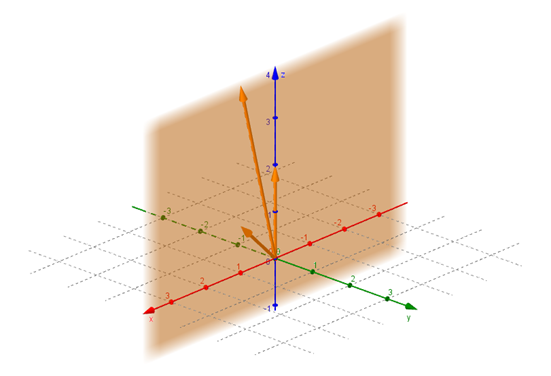
Geométricamente el vector es un vector coplanar con los vectores y . Se puede ver en la siguiente gráfica que pertenecen al plano :
Ejemplo 3
El vector es combinación lineal de los vectores y ya que:
Ejemplo 4
¿Es el vector combinación lineal de los vectores ?
Para responder esto debemos buscar si existen escalares tales que:
Como existen escalares que satisfacen la igualdad entonces es combinación lineal de .
Ejemplo 5
¿Para qué valores de k el vector es combinación lineal de los vectores ?
Para responder esto debemos buscar si existen escalares tales que:
Si la tercera ecuación queda , y el sistema es incompatible. Si entonces se puede obtener .
Entonces para todo el vector se puede expresar como combinación lineal de los vectores dados.

